American Options
American options can be excercised every time until maturity. In most cases, excercise before maturity is not adviseable, because the value of an option is grater than its exercise value. On the other side, if the option value were lower than its exercise value, we would exercise it immidiately, so the value of an option must always be greater or equal to its excercise value. This leads to so called "boundary condition":
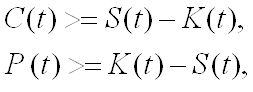
Here is C(t) the value of a call option at the time t, P value of a put option, S the valuie of an underlying and K is the strike of an option. Important for the option value is not only the price of an underlying at maturity: all underlying prices until matrurity may also be important. The expected value of an underlying at some future time point ist equal to its forward price:
,
,
,
.
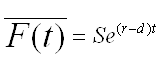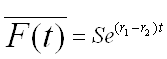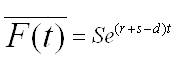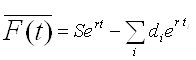We assume here that the distribution of the underlying price is lognormal with mean from above and
standard deviation 
, with
σ as the volatility of the underlying. One good approximation of underlying price movenment
is the binomial tree:
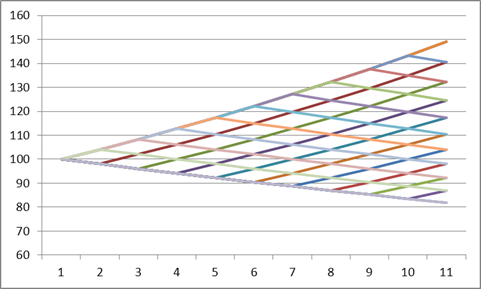
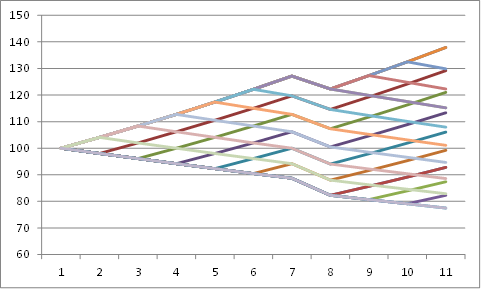
Starting from one node, the price moves with same probability either upwards
,
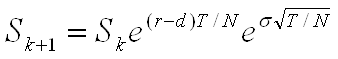or downwards
.
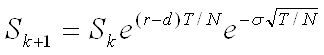This movement has the two important characteristics: the volatility is σ and the mean price is like above described. In order to achieve the valoe of an option we move backwards: On the maturity day, the value is equal to:
,
.
On all other nodes, the value equals to
<
,
.
So, we move backwards, until we reach the starting point and get the value of an option.
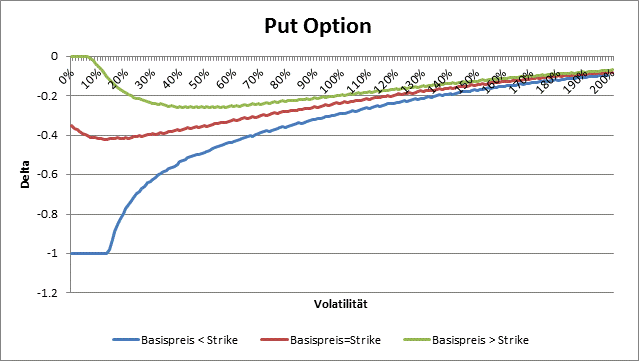
Value and Delta
As already mentioned above, the value of an american call option is always greater than its strike value:
,
.
Otherwise, the value of an american option is always greater than or equal to the value of the same european option. This means
, 
.
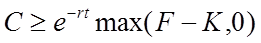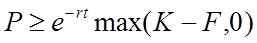The upper boundary is reached by the strike zero for the call option or by underlying price zero by put option. We have
,
.
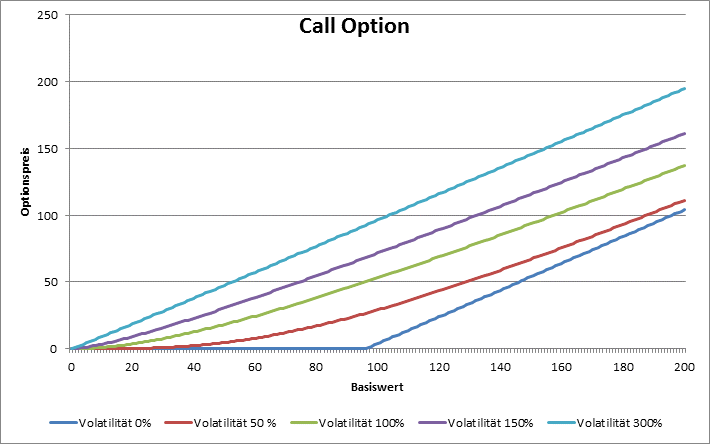
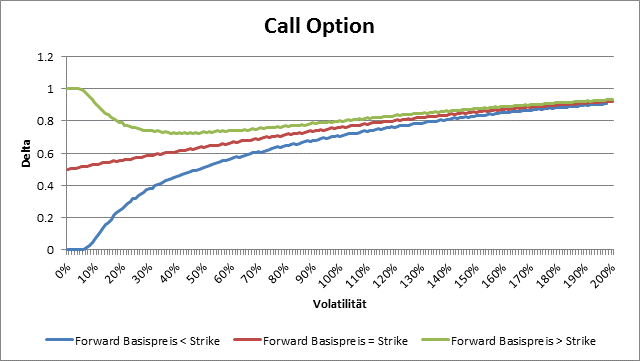
Der limit value for delta of a call option when volatility tends to zero is
- equal zero when the strike is greater than forward,
- somewhere between 0 and 1 when the strike is equal to the forward underlying price, and
- equal one, when the strike is grater than the forward underlying price.
When the volatility tends to infinity then the delta always tends toward one.
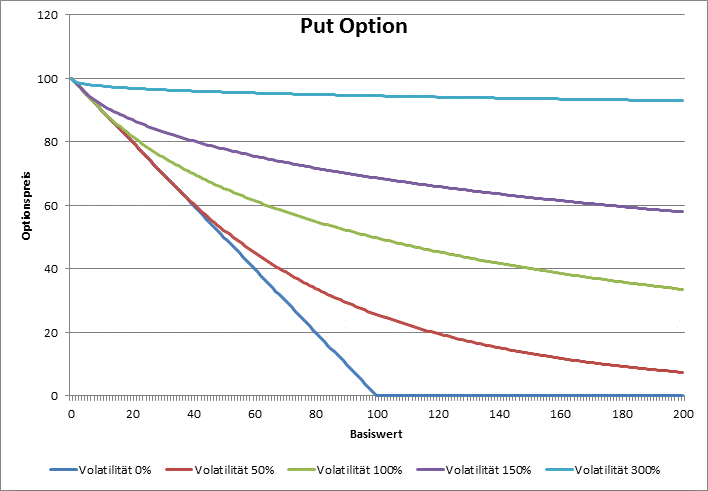
By a put option the limit value for delta when volatility tends to zero is
- equal -1, when the strike is greater than the underlying price,
- somewhere between -1 and 0, when the strike is equal to the underlying price, and
- equal 0, when the strike is lower than the underlying price.
For very big volatilities the delta of a put option tends always to zero.
