Barrier Options

Barrier options are european options with additional price barriers. The right to exercise an option depends also on, if the underlying price crrosed the barrier at least once (=Knock-In) resp. not at all (=Knock Out). If we have only one barrier (sometimes there are two) and the underlying price is lower than the barrier, then we call the Knock Out Option also Down & Out Option and Knock In Option we call Down & In Option. Analogously we have Down & Out Option and Down & In Option, if the underlying price is upper than the strike.

Valuation

We value barrier options with Monte-Carlo Simulation. We assume that the underlying price maks the so called Geometric Brownian Motion:

We call the factor µ Drift, and σ is called volatility. The is a random process (Wiener process) with expentance 0 and variance 1. As by the european option, the drift µ equals r-d for equity index options (r = risk free discount rate, d dividend yield), by FX options ( is discount rate for doemstic resp. foreign currency), and r+s-d by commodity options (r=discount rate, s=storage costs, d=conviniency yield).

In Monte Carlo Simulation, we simulate the geometric Brownian motion by discrete steps. The time to maturity of option is divided in K small steps. (We will set K as number of days in our calculator) and the motion of the underlying price is „diskretized“ in the following way

Hereby is the so called Gaussian Random Number (a random real number choosen in the way, that its expectation is 0 and variance 1). We repeat random motion many times (in our calculoator 5000 times). Every time on the end of the motion we calculate the payoff. E.g. for a Knock-Out Call Option we have:

The value of option is then:

Option Price

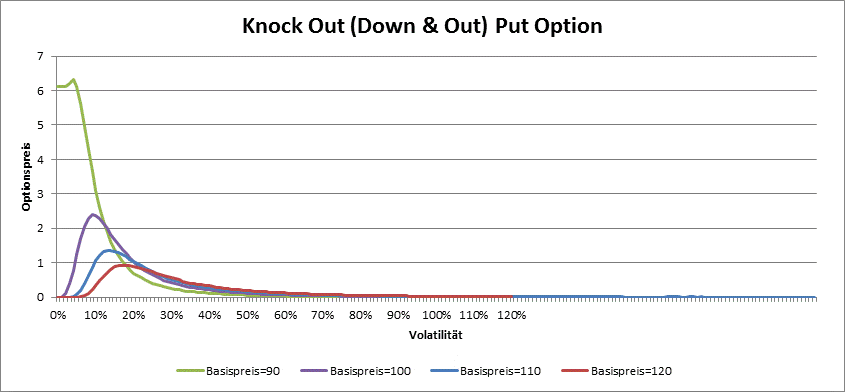
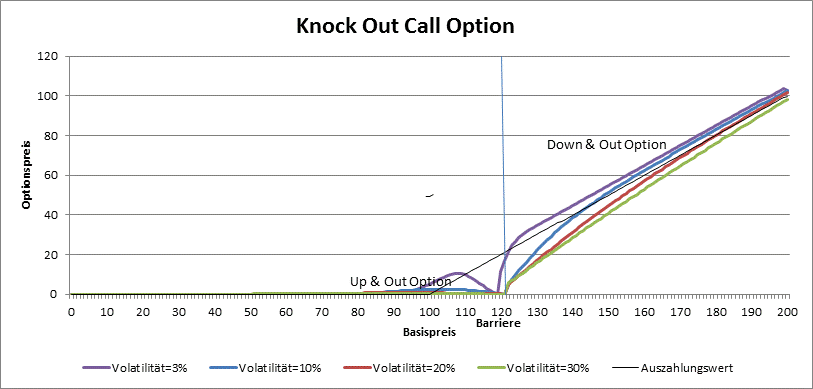
The price of barrier option do not depend only on dicount rate, maturity, strike, underlying price and volatility, it also depend on the position of the barrier. By Knock-Out options for example, the rule the bigger the volatility, the bigger the price, do not hold, because for greater volatilities is the probability that the barrier is knocked also bigger. So it is possible that the value of a Up & Out Call or Down & Out Put option do not cross some amount independently of underlying price or volatility.

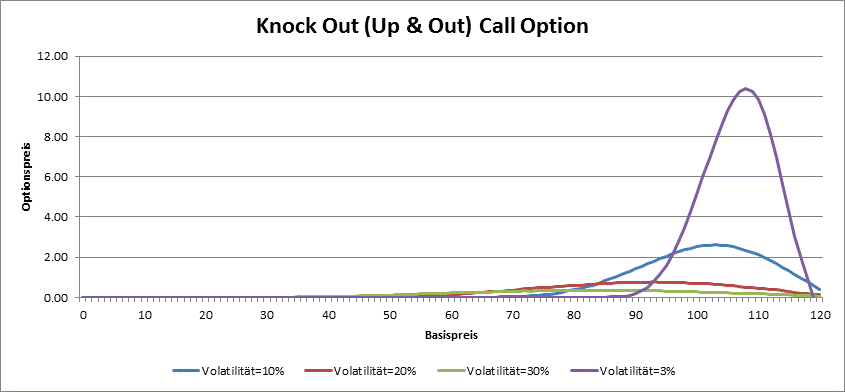
Far away from the barrier the Down & Out call and Up & Out Put options behave like plain (vanilla) options.

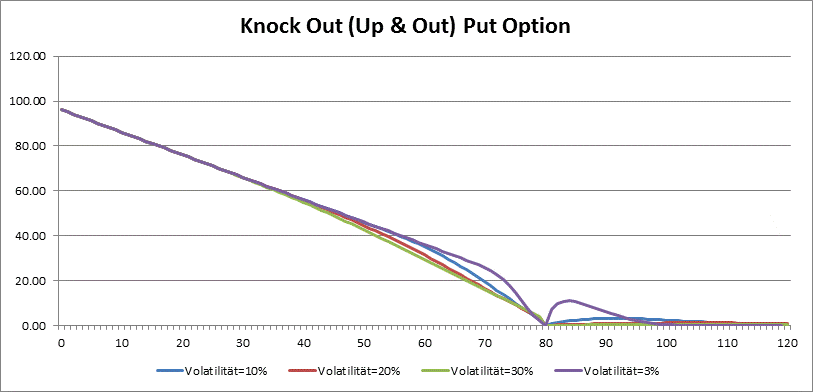
By Knock Out options is vega not always positive. The higher the volatility, the greather the probability that the barrier is crossed, so the price is smaller. Only by very low volatility the barriar options behave like plain options and have positive vega.

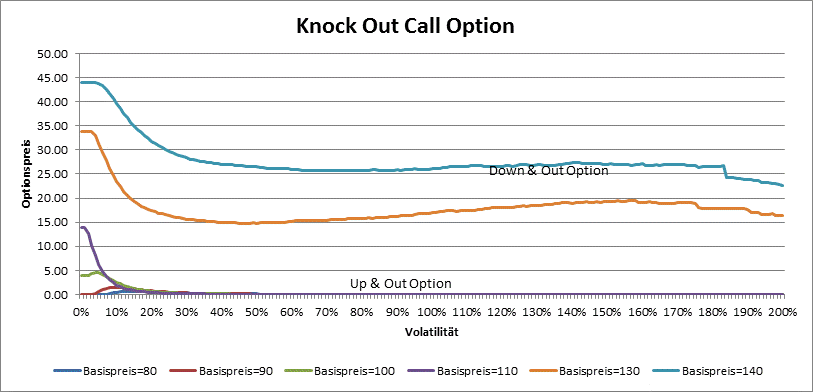
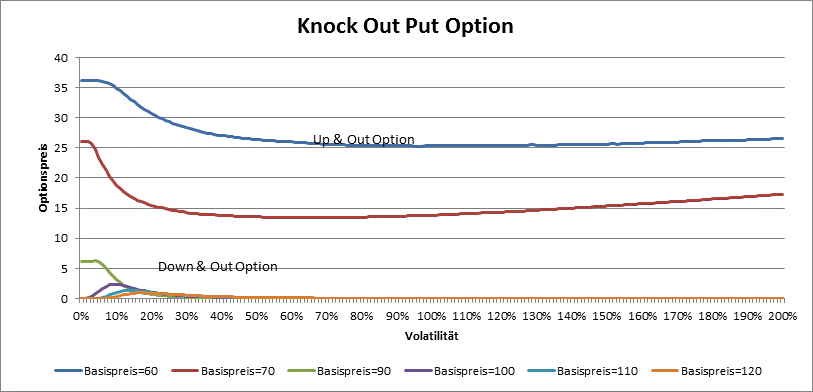
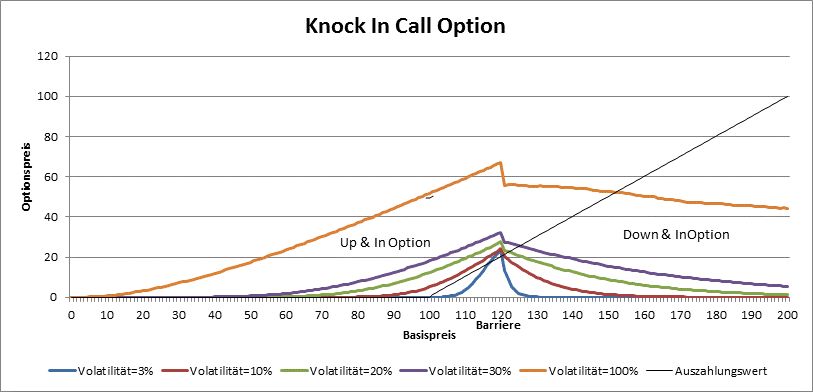
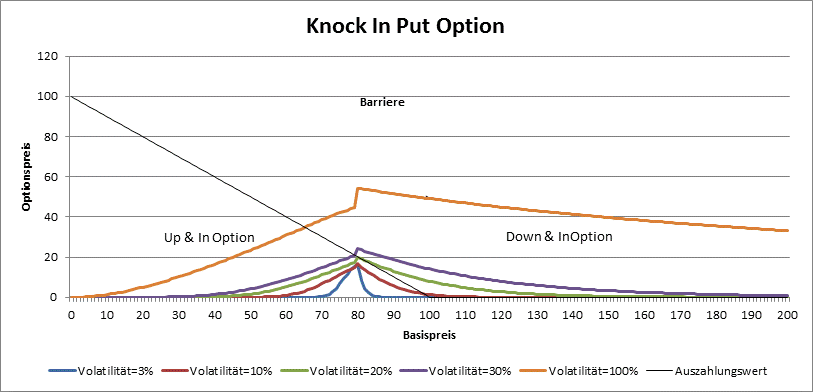
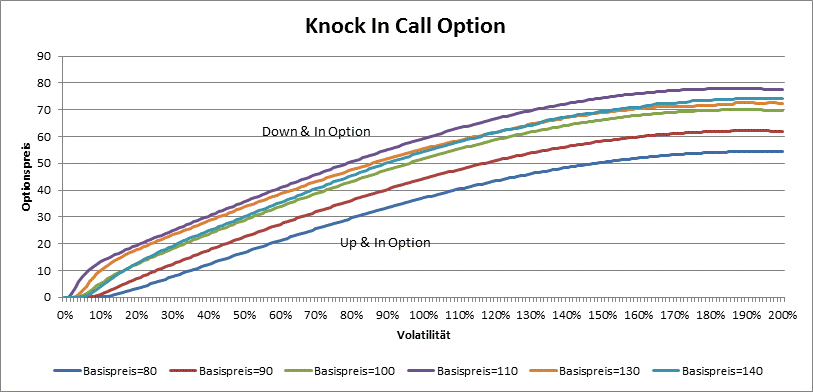
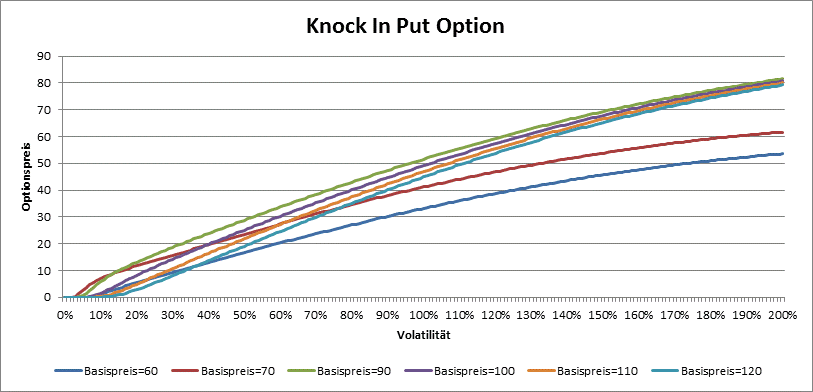
By knock in options, the price is around the barrier the greatest. Vega is always positive.