European Options

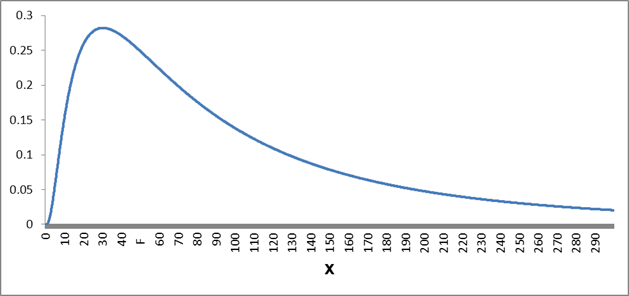
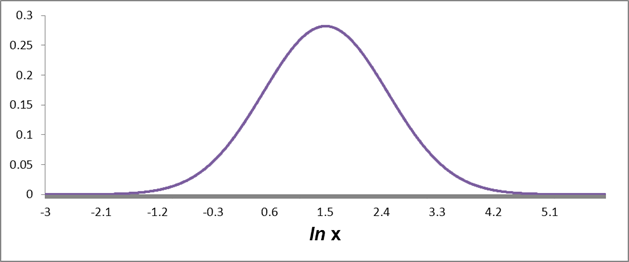
European options can be exercised only at their maturity day. Therefore, their value depends only on the underlying price at maturity. We do not know this price in advance, we can only estimate the probability distribution on this day. We assume that this dirtribution is a Log-normal distribution around the forward price of an underlying.

Here is F forward underlying price, σ volatility and t time to maturity in years.

Under these assumptions, we can value the option through the Black and Scholes formula:

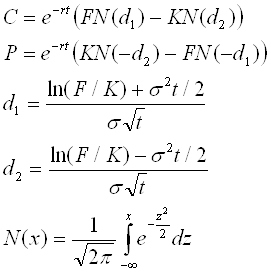
Here is C the value of a call option, P value of a put option, r is the risk free discount yield, t is time to maturity in years, F is underlying forward price and K is is Strike.

By an onption on an equity index, the formula for the underlying forward price is

Here is S the underlying price and d dividend yield of the equity index. By FX options, the underlying formard price equals to

Hereby is S the current exchange rate, r₁ the risk free interest rate in the domestic currency (the currency in which we value the option) and r₂ the risk free interest rate of foreign currency. By commodity options we usually do not have fixed formula for dependency between current and forward underlying price, we just have to know it. In some (seldom) cases the dependency between them is given by

Here is s the storage yield and d convinience yield.

Price and Delta

The option price depends on underlying forward price, strike, maturity in years, discount interest rate and underlying volatility. Strike and maturity are part of option contract, underlying forward price and discount interest rate can be observed on market, only by the volatility we have some wiggle room. The volatility need not to be the historical price deviation (historical volatility), it is the expectation of future price oscilations from market players. We cannot measure or observe it, we can only implicitly derive it from option price.

In option price calculator (next part) we can derive the volatility if option price or its delta are known. For hedging purposses we can also estimate the strike if all other parameters are known.

Irrespective of choosen volatility, not all option prices and deltas can be reached. By a call option the lowest possible price is reached when we set volatility to zero. It is the discounted exercise value:

The call option price is always lower then the price of an option with zero strike. By strike equal to zero the price of call option equals to its forward price. We have then

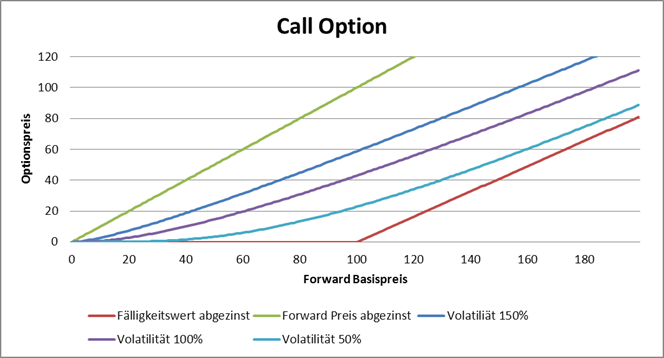
By a put option we follow the same logic and get

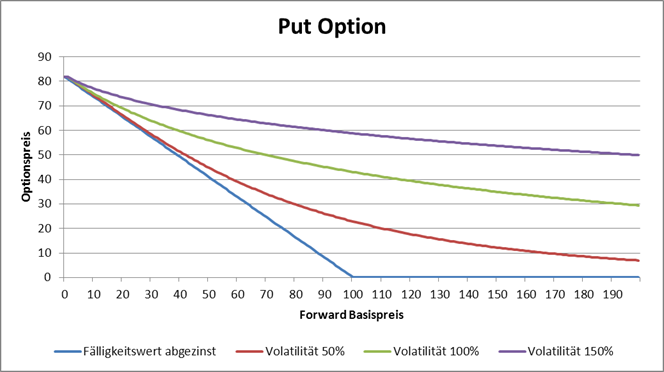If the underlying forward price is lower than strike, then the lowest delta of option is reached by volatility equal to zero and the highest delta is reached when volatility tends to infinity. We have

by the call option and

by the put option. If the underlying forward price equals to the strike we have the same situation, only the delta by the volatility zero ist not zero then we have

by the call option and

by the put option. If the underlying forward price is greather than strike, we have the same values for the delta at zero and at infinity.

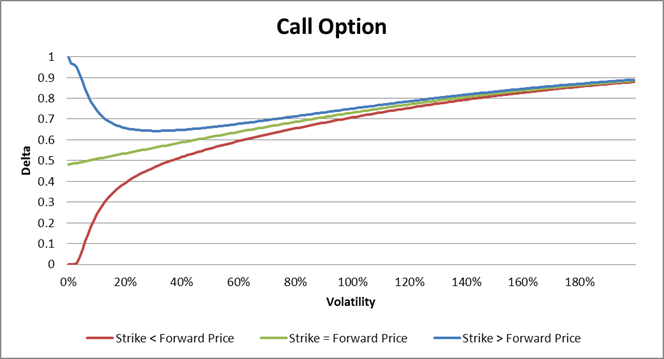
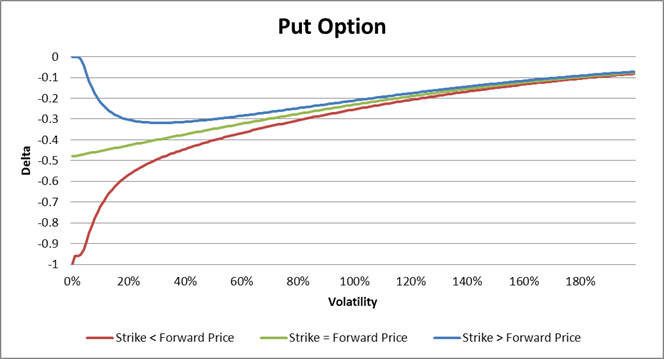
In case of an equity option with estimated future dividend dates and dividend values, the underlying forward price is

Here are d_i-s the future dividends between value day and maturity and t_i is time distance in years between the i-th ex-dividend day and maturity in years.