Barrier-Optionen

Barrier-Optionen sind europäische Optionen, die zusätzlich eine oder zwei Preisschwellen (Barrieren) haben. Das Recht, eine Option auszuüben, hängt auch davon ab, ob der Basispreis während der Laufzeit die Preisschwelle(n) mindestens einmal (=Knock-In) bzw. überhaupt nicht (=Knock Out) überschritten hat. Wenn wir nur eine Preisschwelle haben, und diese befindet sich oberhalb des Ausübungspreises, dann heißt die Knock-out Option auch Up & Out Option und die Knock In Option heißt dann auch die Up & In Option. Analog dazu haben wir auch Down & Out bzw. Down & In Optionen, wenn die Preisschwelle unterhalb des Ausübungspreises liegt.

Die Bewertung

Barrier-Optionen bewerten wir mit der Monte-Carlo Simulation. Angenommen wird, dass sich der Basispreis während der Laufzeit die sog. Geometrische Brownsche Bewegung bewegt:

Dabei nennen wir den Faktor μ Drift, und σ heißt Volatilität. Der W_t ist ein Zufallsprozess (Wiener-Prozess) mit Erwartung 0 und Varianz 1. Wie bei der europäischen Option ist der Drift μ gleich r-d für die Aktienindex-Optionen (r = risikoloser Zinssatz, d die Dividendenrendite), r₁-r₂ bei den FX-Optionen (r_i ist der Zinssatz der Heim- bzw. Fremdwährung), r+s-d bei den Rohstoff-Optionen (r=Zinssatz, s=Lagerhaltungskosten, d=Prämie für die schnelle Lieferung).

Bei der Monte Carlo Simulation simulieren wir die Geometrische Brownsche Bewegung durch diskrete Schritte. Die Laufzeit der Option wird in K kleine Schritte geteilt. (Bei uns wird K Anzahl der Tage sein) und die Bewegung des Basiswertes wird „diskretisiert”

Dabei ist W_k die sog. Gaußsche Zufallszahl (eine reale Zahl, so gewählt, dass die Erwartung von Zufallszahlen 0 und die Varianz 1 sind). Die Zufallsbewegung wird mehrmals wiederholt (bei uns 5000-mal). Jedes Mal wird am Ende der Zufallsbewegung der Zahlbetrag (engl. Payoff) berechnet. Z.B. bei einer Knock-Out Call Option haben wir:

Der Wert der Option ist dann gleich:

Der Optionspreis

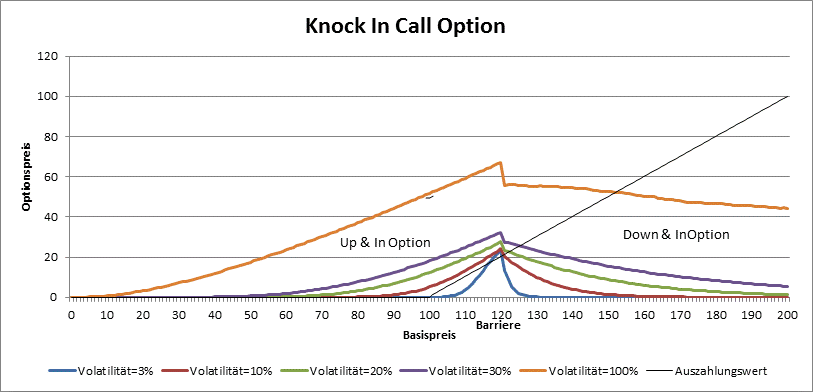
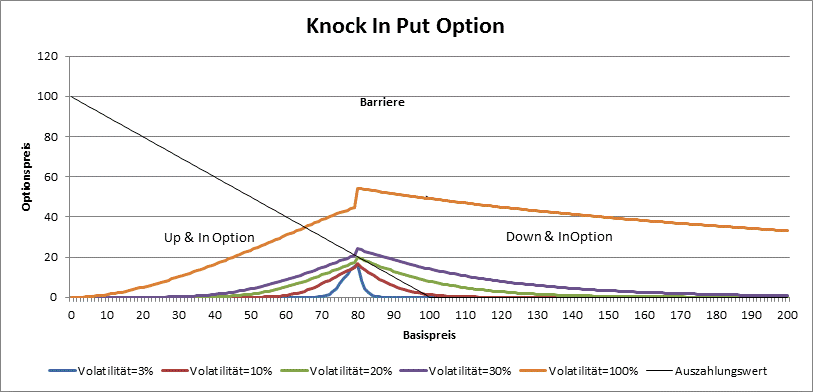
Die Preisbildung bei den Barrier-Optionen hängt nicht nur von Diskont-Zinssatz, Laufzeit, Ausübungspreis und Volatilität, sondern auch von der Barriere ab. Bei der Knock-Out Optionen z.B. gilt die Regel nicht, je grüßer die Volatilität, desto grüßer der Preis: bei grüßeren Volatilitäten ist die Wahrscheinlichkeit, dass die Barriere überschritten wird auch grüßer und dies wirkt sich preismindernd aus. So kann z.B. der Preis bei einer Up & Out Call oder Down & Out Put Option eine Schwelle unabhängig vom Basispreis und Volatilität nicht überschreiten.

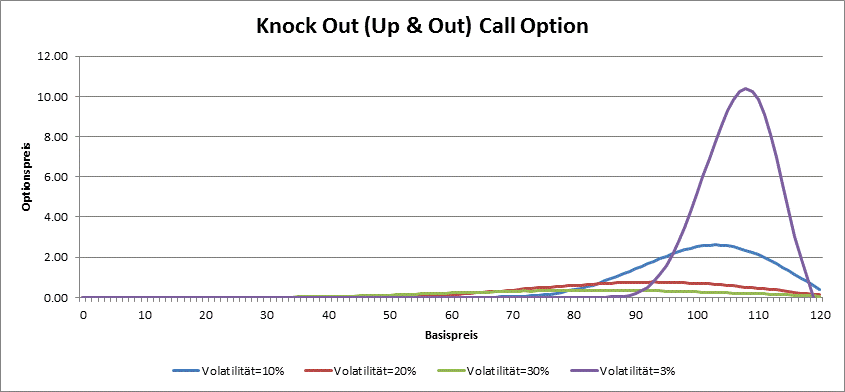
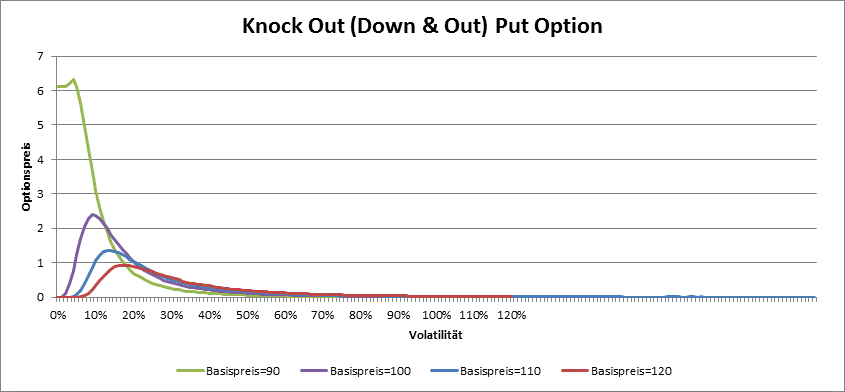
Weit von der Barriere verhalten sich die Down & Out Call und Up & Out Put Optionen wie die normalen (Plain Vanilla) Optionen.

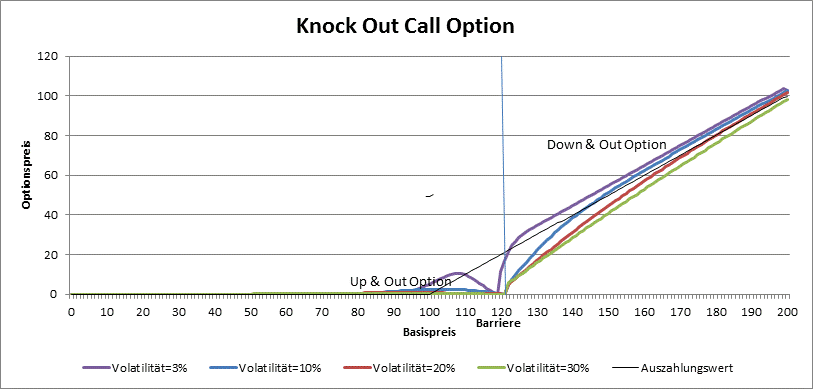
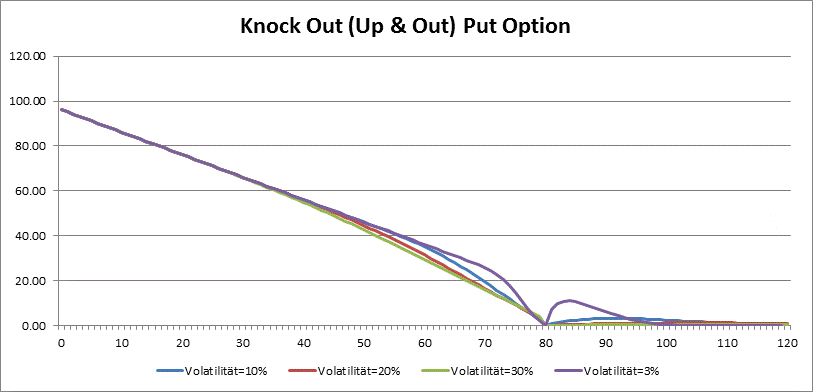
Bei den Knock Out Optionen ist Vega nicht immer positiv. Es gilt, je grüßer die Schwankung, desto grüßer die Wahrscheinlichkeit, dass die Barriere überschritten wird, also der Preis wird kleiner. Nur bei den sehr kleinen Volatilitäten verhalten sich die Barrier Optionen wie die normalen Optionen und haben ein positives Vega.

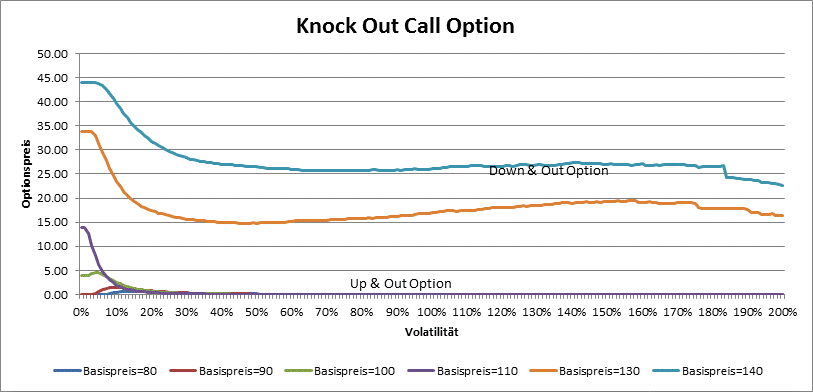
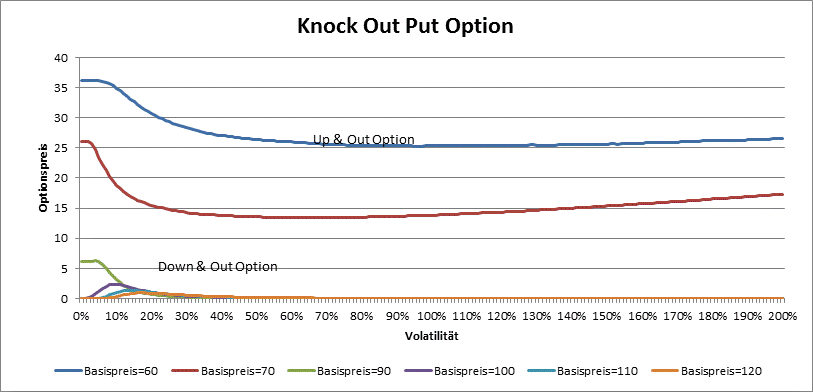
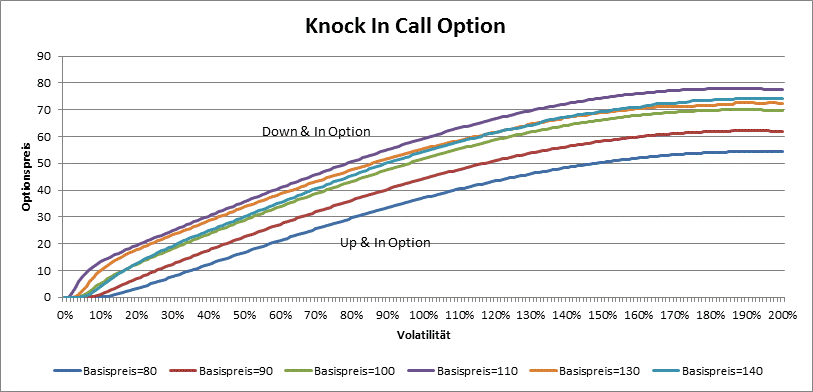
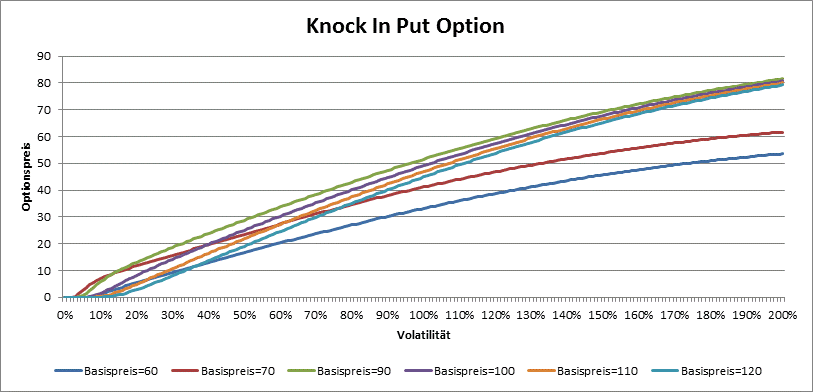
Bei den Knock-In Optionen ist der Preis rund um die Barriere am grüßten. Das Vega ist immer positiv.