Europäische Optionen
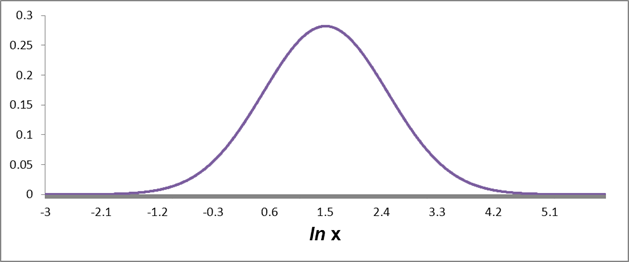
Die Europäischen Optionen können nur an ihrem Fälligkeitstag ausgeübt werden. Somit hängt der Wert dieser Optionen nur von dem Kurs des Basiswertes am Fälligkeitstag selbst. Diesen Kurs wissen wir nicht im Voraus. Wir können nur die Wahrscheinlichkeitsverteilung des Kurses schätzen. Wir unterstellen zunächst, dass diese Verteilung eine Log-normale Verteilung rund um den Forward-Basispreis ist.

Hierbei ist F der Forward-Basispreis, σ die Volatilität und t die Laufzeit in Jahren.

Unter diesen Voraussetzungen kann der Preis dieser Option durch die Formel von Black und Scholes berechnet werden:
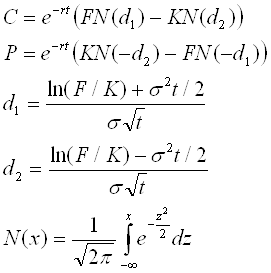
Hierbei ist C Preis einer Call-Option, P Preis einer Put-Option, r ist der risikolose Diskont-Zinssatz, t ist die Laufzeit in Jahren, F ist der Forward-Basispreis und K ist der Ausübungspreis (Strike).
Bei einer Option auf einen Aktienindex ist die Formel für den Forward-Basispreis gleich
![]()
Hier ist S der Basispreis und d die Dividendenrendite des Index. Bei den FX-Optionen ist der Forward-Basispreis gleich:
![]()
Dabei ist S der jetzige Umtauschpreis, r1 der risikolose Zinssatz der heimischen Währung (der Währung in der die Prämie bezahlt wird) und r2 der risikolose Zinssatz der Fremdwährung. Bei den Rohstoff-Optionen gibt es normalerweise keinen festen Zusammenhang zwischen dem Basispreis und dem Forward-Basispreis. Wir müssen dann den Forward-basispreis einfach wissen. In einigen (seltenen) Fällen lautet der Zusammenhang:
![]()
Dabei ist s der Satz für Lagerhaltungskosten und d die Prämie, wenn man sofortige Lieferung wünscht (engl. „Convinience Yield“).
Preis und Delta
Der Preis einer Option hängt vom Forward-Basispreis, vom Ausübungspreis, von der Laufzeit in Jahren, vom Diskont-Zinssatz und von der Volatilität der Option ab. Ausübungspreis und Laufzeit in Jahren sind Teil des Option-Vertrages, Forward-Basispreis und Diskont-Zinssatz können am Markt beobachtet werden, nur bei der Volatilität gibt es Interpretationsspielräume. Diese Volatilität ist nicht etwa die Schwankung des Basispreises in der Vergangenheit, sondern seine von den Marktteilnehmern erwartete „künftige“ Schwankung. Diese Schwankung kann man nicht messen oder beobachten sondern nur implizit aus dem Preis herauslesen.
Im Kalkulator (nächter Abschnitt) kann man diese implizite Berechnung der Volatilität durchführen, wenn neben allen anderen Parametern auch der Optionspreis oder Delta bekannt sind. Für Absicherungszwecke kann man auch die implizite Berechnung von Ausübungspreis machen, wenn alle anderen Parameter bekannt sind.
Unabhängig von der Volatilität können nicht alle Preise und Deltas erreicht werden. Bei einer Call Option wird der kleinste preis bei der Volatilität gleich Null erreicht: es ist der diskontierte Ausübungswert:
![]()
Der Optionspreis ist immer
kleiner als der Optionspreis für eine Option mit dem Ausübungspreis gleich
Null, und beim Ausübungspreis gleich Null ist der Optionspreis gleich der
diskontierte Forward-Basispreis unabhängig von der Volatilität. Daraus folgt
dann
![]()
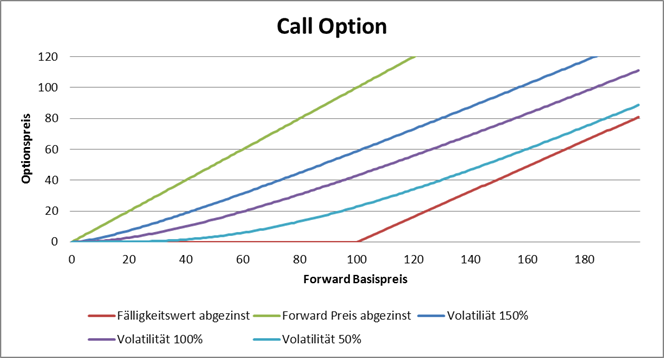
Bei der Put Option folgen wir der gleichen Logik und erhalten
![]()
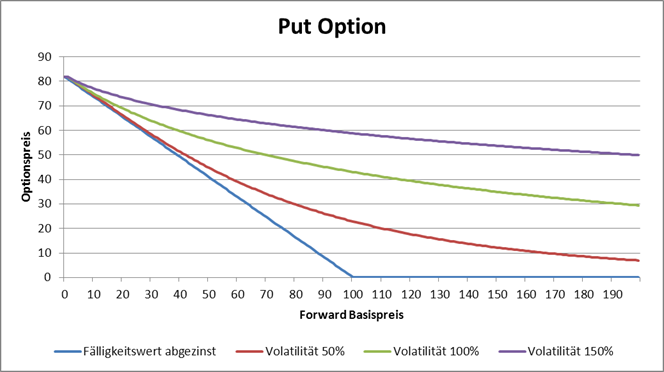
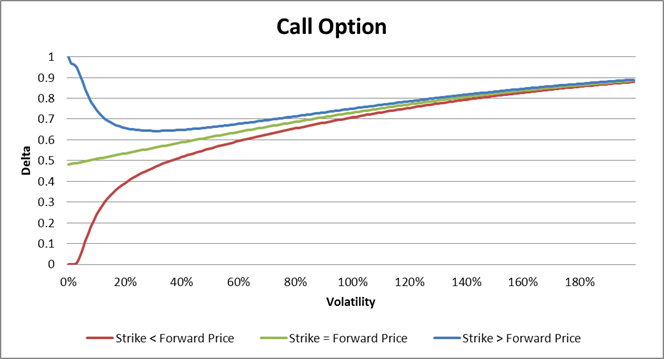
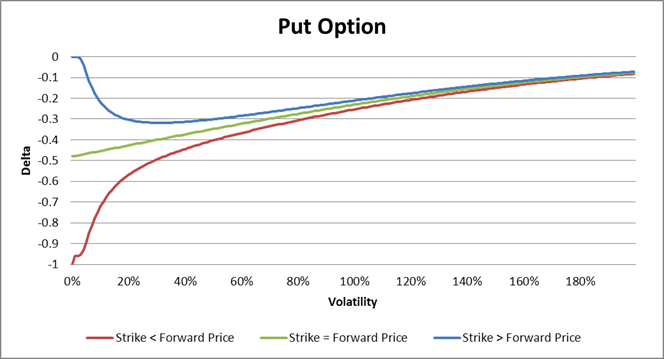
Wenn der Forward-Preis kleiner als Ausübungswert ist, dann ist Delta der Option am kleinsten bei der Volatilität gleich Null und am größten wenn Volatilität gegen Unendlich strebt. Damit erhalten wir
![]()
bei der Call-Option und
![]()
bei der Put Option. Wenn der Forward-Preis gleich dem Ausübungswert ist, gilt das Gleiche, nur der Grenzwert für Volatilität gleich Null ist nicht Null sondern es gilt
![]()
bei der Call-Option und
![]()
bei der Put-Option. Wenn der Forward-Preis größer als der Ausübungswert ist, dann wird die obere Grenze von Delta sowohl, wenn die Volatilität gegen Null, als auch gegen Unendlich strebt, erreicht. Das kleinste Delta wird dann mittels Bisektionsmethode ermittelt.
Im Fall einer Aktienoption, wo die künftigen Dividenden geschätzt werden können, ist der Forward-Basispreis gleich

Dabei sind die di-s die künftigen Dividenden zwischen Valuta und Fälligkeit, und ti ist der zeitliche Abstand zwischen der i-ten Dividende und Fälligkeit in Jahren.
